Mapping Reads I


mapping suffix tree BWT

WarmUp with Python Numbers

In the previous lecture we uploaded data and performed QC. The outcome of this analysis is a set of Illumina reads that are ready to be mapped. Before we map we should understand the theory behind this process.

Mapping versus alignment

One possible idea on how to speed things up will be to first find most likely locations for each read and them refine alignments as necessary. In other words reads should be mapped by identifying regions of the genomes from which they most likely originate. The term mapping is sometimes used interchangeably with the word “alignment”. Yet mapping and alignment are somewhat different concepts. Heng Li defines them this way:

So let’s see how we can find potential read locations quickly. Below is a list of key publications highlighting basic principles of current mapping tools:

Indexing and substrings

Indexing is not a new idea. Most books have an index where a word is mapped back to a page where it is found. This particular type of index is called inverted index. The word inverted implies that there is also a non-inverted or forward index. The image below explain the distinction between the two:
Inverted index
Forward index. (From Wikipedia).

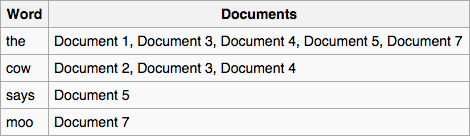
For what we are interested in (searching for the best location of a read in the reference genome) we will use inverted index. We will refer to it simply as index. So to find a pattern in a string using an index we first need to create that index. To create an index for a string T (i.e., a genome) we will need to:
Creating an index. From Ben Langmead

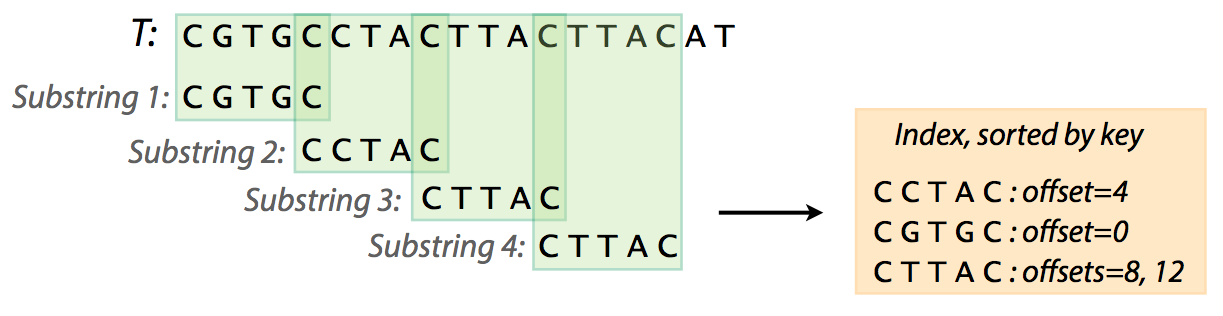
Now that we’ve created an index for text T = CGTGCCTACTTACTTACAT we might as well search it. Suppose we now want to find whether a pattern CTACTTAC (we will refer to pattern as to P) is present in T. To do this we need:
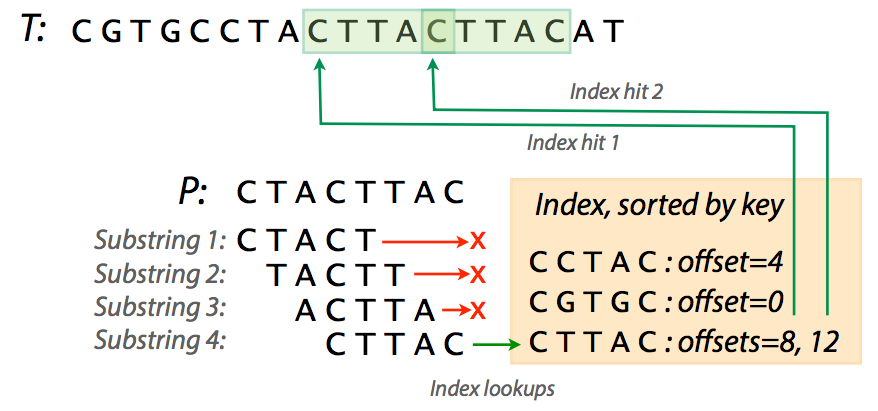Looking for P in T. The first three substrings don’t have a match. Image from Ben Langmead.

In the figure above you can see that trying various substrings from P yields three failures and a success with two hits. Of course in our case the T is very short and you can easily see that an index for a realistic fragment of DNA can be very large. For example, an index for human chromosome 1 (~249,000,000 nucleotides) will occupy over 12 GB of space. In these cases a practical solution may be skipping some of the substrings while making the index. For instance, including only every 4th substring (i.e., using interval of 4) in a human chromosome 1 index will reduce memory usage to a peak of ~8Gb.

As one can see finding patterns in text using indexes requires finding values for parameters such as substring length and the interval (if we use skipping). These value have significant implications to the speed of the search, memory use, and , importantly, to specificity. The following table shows how choosing different values for substring length and interval affect speed, memory footprint, and specificity for finding pattern GCGCGGTGGCTCACGCCTGTAATCCCAGCACTTTGGGAGGCCGAGGCGGG

within human chromosome 1 (data from here):

Substring length Interval Indexing time (s) Search time (s) Memory usage (Gb) Specificity (%)
4 4 59.31 0.40 ~7.6 0.12
7 7 63.74 0.06 ~5.0 1.26
10 10 72.52 0.02 ~3.6 4.11
18 18 40.20 0.02 ~2.1 4.37
30 30 19.78 0.00 ~1.6 11.72

Specificity can be thought of as a proxy for the number of times an index hit can be extended to a true match between T and P. The figure below explain this idea:

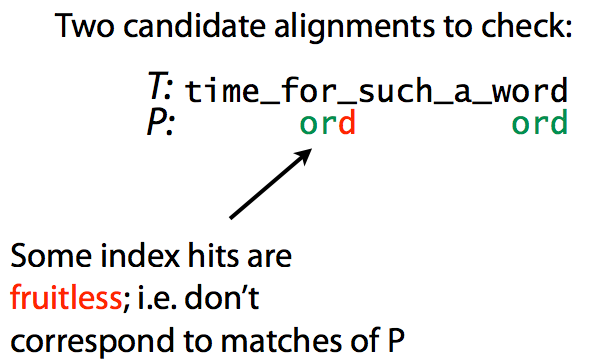Specificity. Matching ord to time_for_such_a_word. Image from Ben Langmead

here we look for pattern ord within text time_for_such_a_word. The first index hit does not produce a match, while the second does. Decreasing the number of fruitless hits increases specificity and speeds up the search. Intuitively, this is achieved by increasing the substring length.

In summary, we have seen that we can create an index (a map) containing coordinates of substrings from a text T. We can then use this map to find occurrences (if they exist) of pattern P within the T. The map can be represented in variety of ways including sorted lists, hash tables, and trees:
Sorted list
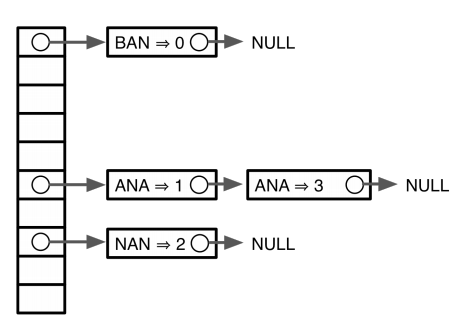Hash
Trie
Sorted list (top), Hash (middle), and Trie (bottom). From Ben Langmead and Wikipedia.

What’s important here is that sorted lists and especially hash tables provide a quick way to find the initial hit, but they are limited by the choice of the substring size. We’ve seen before (the Specificity table above) that the choice of substring size will have profound effects on the performance of the search. Would it be nice if we would not need to make that choice. For this we will continue to Tries and Trees below.

Tries and trees

Let’s consider text T = gtccacctagtaccatttgt. Using the logic from previous section we can build an index using substrings of length 2 with interval 2 (skipping every other substring) that would look like this after sorting:

Substring Offset
ac 4
ag 8
at 14
cc 12
cc 2
ct 6
gt 18
gt 0
ta 10
tt 16

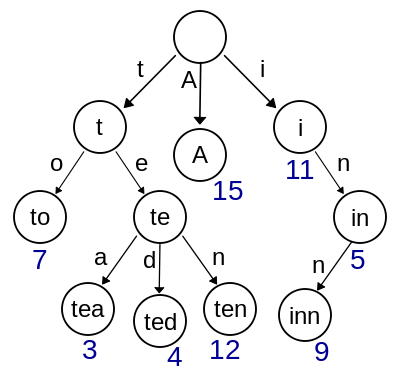
Representing this sorted list as a trie that would map substrings to their positions (offsets) will look like this:
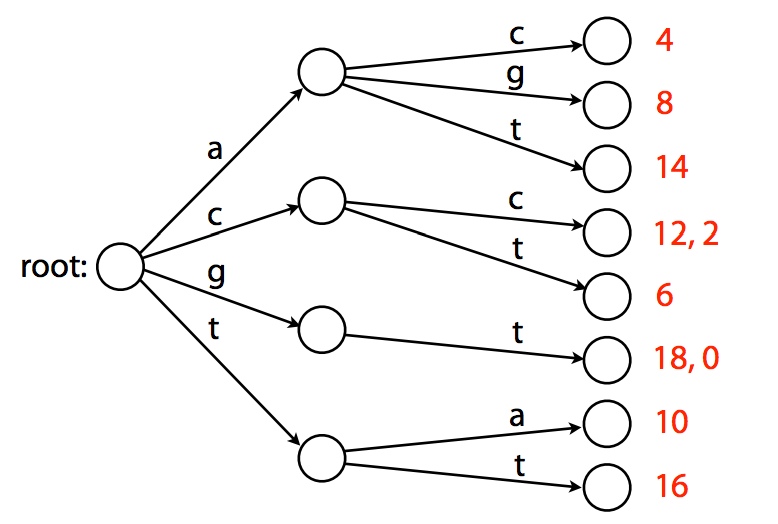A trie. Example from Ben Langmead.

Note that this trie is the smallest tree (trie versus tree is indeed a bit confusing) representing a collection of substrings that has the following properties:

While the above example shows how we can quickly find positions for a given substring, it still relies on a fixed substring length. To see how we can deal with this limitation let’s introduce the idea of indexing with suffixes rather than with fixed substrings. Consider the following text T = GTTATAGCTGATCGCGGCGTAGCGG. Let’s add a special symbol $ to the end of this text. For T$ a list of all substrings will look like this:

GTTATAGCTGATCGCGGCGTAGCGG$
 TTATAGCTGATCGCGGCGTAGCGG$
  TATAGCTGATCGCGGCGTAGCGG$
   ATAGCTGATCGCGGCGTAGCGG$
    TAGCTGATCGCGGCGTAGCGG$
     AGCTGATCGCGGCGTAGCGG$
      GCTGATCGCGGCGTAGCGG$
       CTGATCGCGGCGTAGCGG$
        TGATCGCGGCGTAGCGG$
         GATCGCGGCGTAGCGG$
          ATCGCGGCGTAGCGG$
           TCGCGGCGTAGCGG$
            CGCGGCGTAGCGG$
             GCGGCGTAGCGG$
              CGGCGTAGCGG$
               GGCGTAGCGG$
                GCGTAGCGG$
                 CGTAGCGG$
                  GTAGCGG$
                   TAGCGG$
                    AGCGG$
                     GCGG$
                      CGG$
                       GG$
                        G$
                         $

Recall that a trie has the following properties:

Let’s now use these rules to build a suffix trie for a much simpler text T = abaaba. It is much smaller than the text we used above and so it will be easier to get the point across. First, let’s add $ and create a list of all suffixes:

abaaba$
 baaba$
  aaba$
   aba$
    ba$
     a$
      $

now let’s create a trie:

Looking for substrings in a Trie
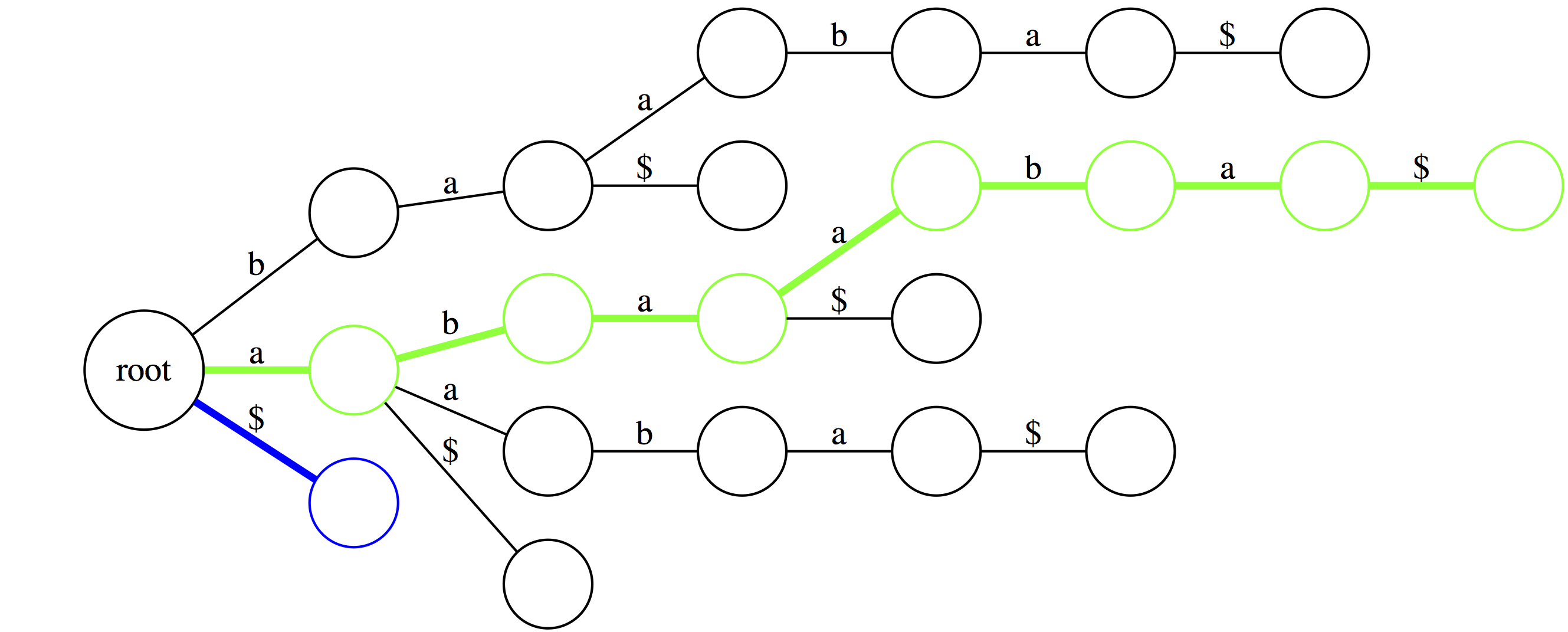The green path shows the longest suffix (the entire thing). The blue path is the shortest suffix containing only the terminal character.
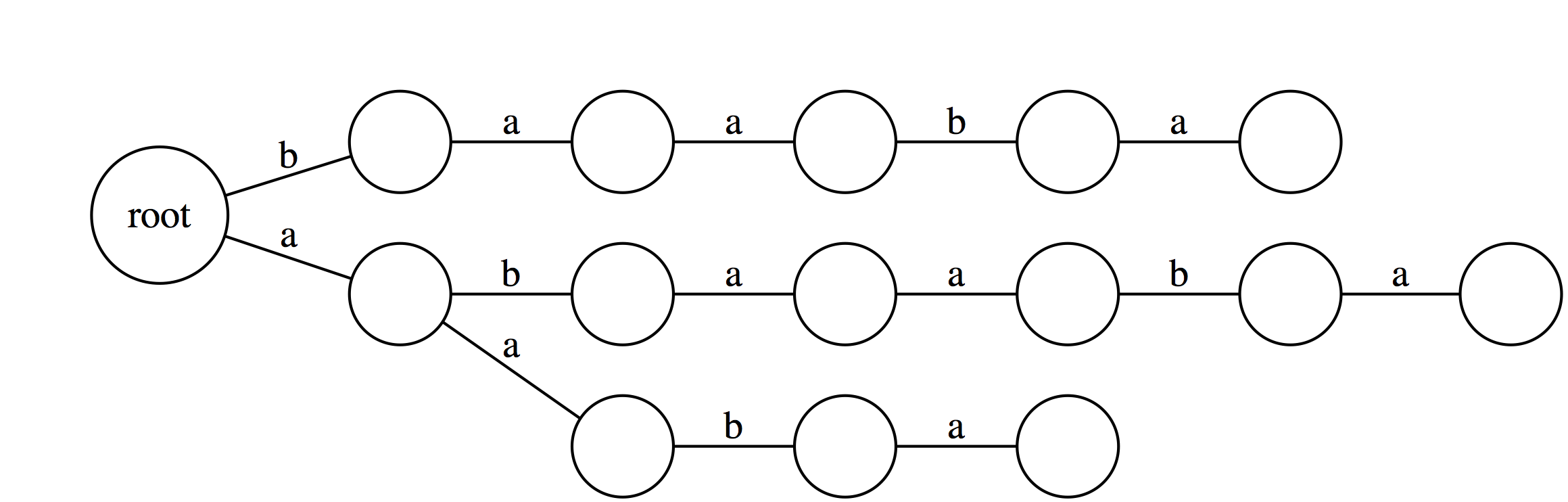Note, that the trie would look dramatically different had we not added the $ at the end. The difference is that without the $ the trie will not have every suffix to be represented by a path from root to a leaf.
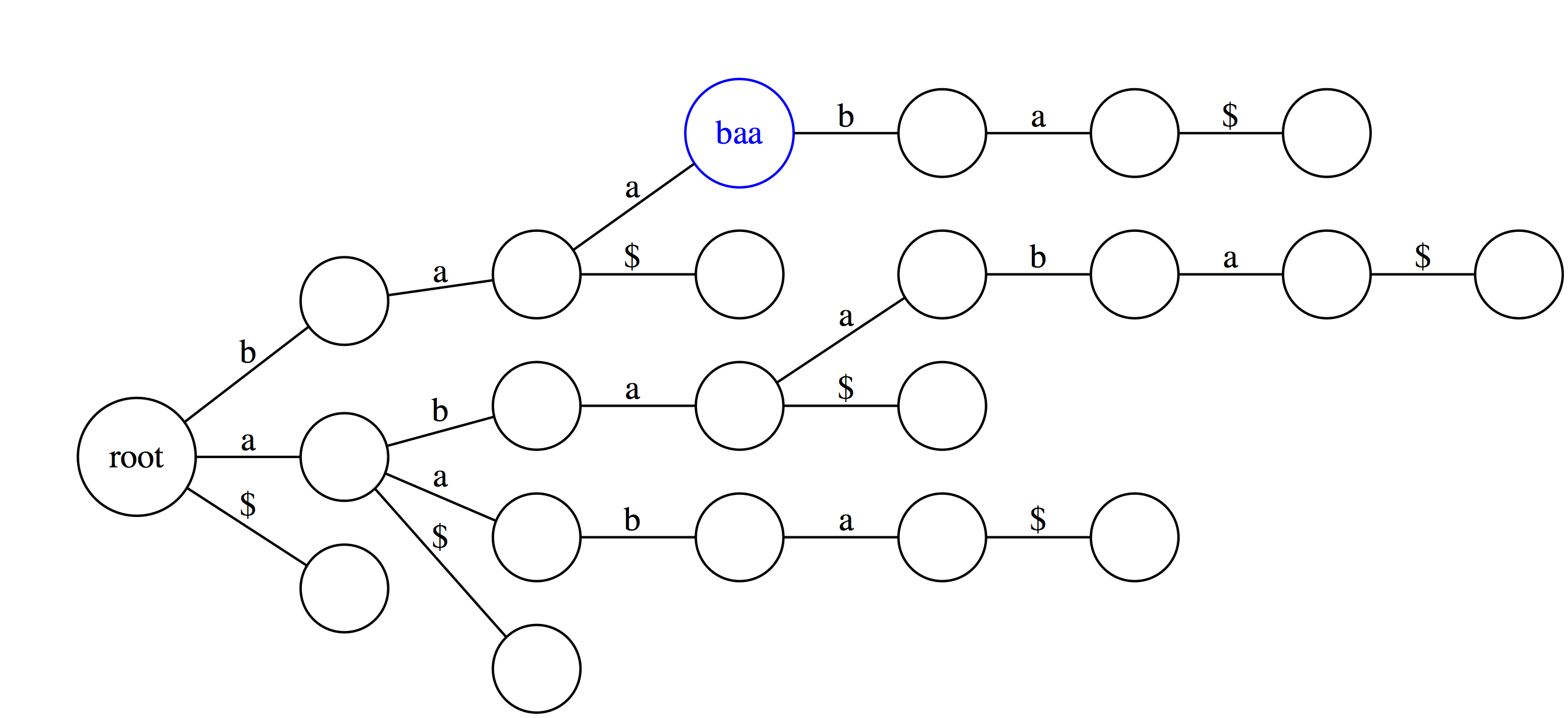In suffix trie every edge is labeled with a single character and nodes have no labels in our representation. However, you can think of every node as being labeled with a string that spells out all characters occurring along a path from the root up to the that node. For example, the blue node baa spells out characters b, a, and a along a path from the root.
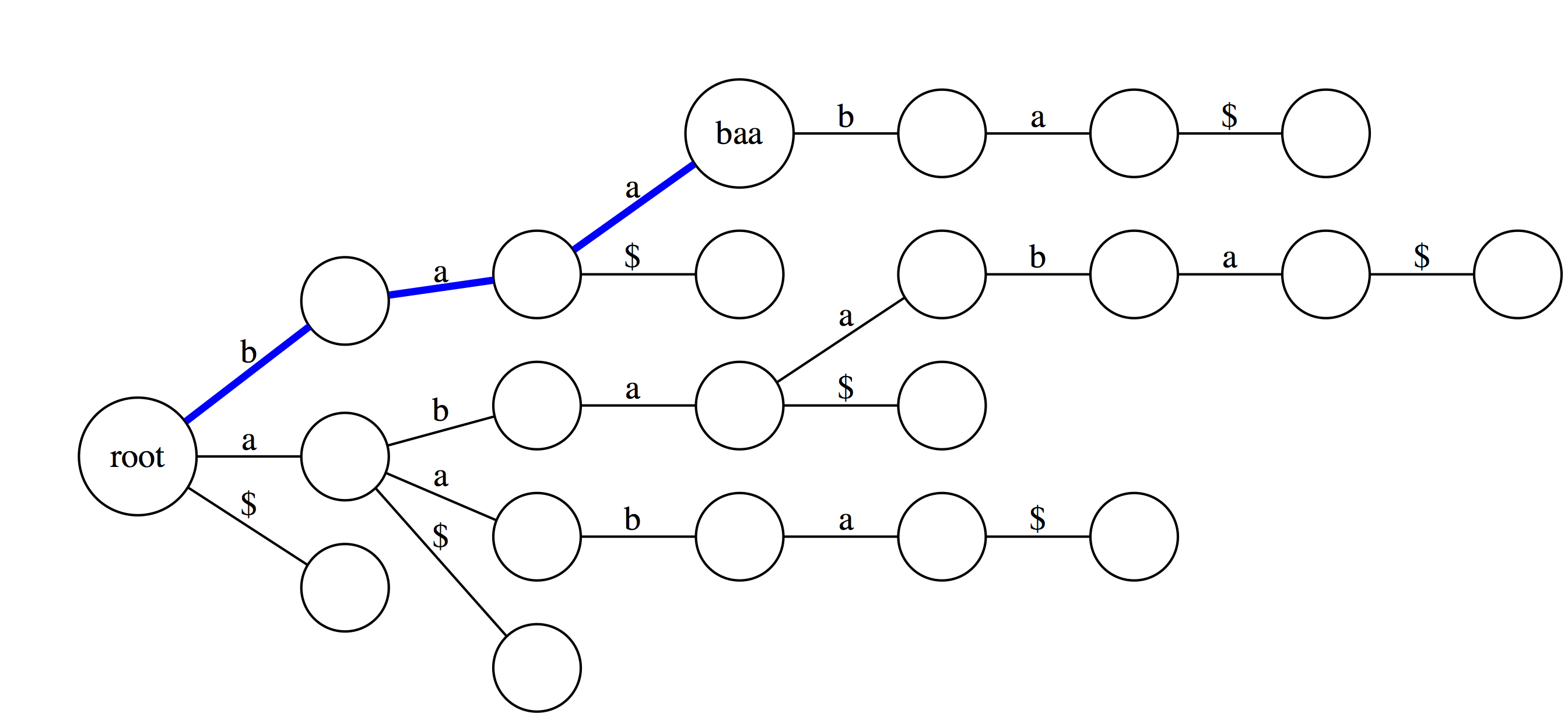Suffix trie is an ideal data stricture to quickly check if a pattern is or is not present in a text. The following three examples highlight how this can be done. Suppose we want to check if a substring baa is present within text abaaba represented as our suffix trie. We start at the root and take an edge labeled with b. We next proceed through an edge labeled a. At this point there are two outgoing edges: a and $. Since the last character in baa is a we take the edge labeled as a. Because the entire substring baa can be spelled out as a path from the root we conclude that baa is indeed a substring of abaaba.
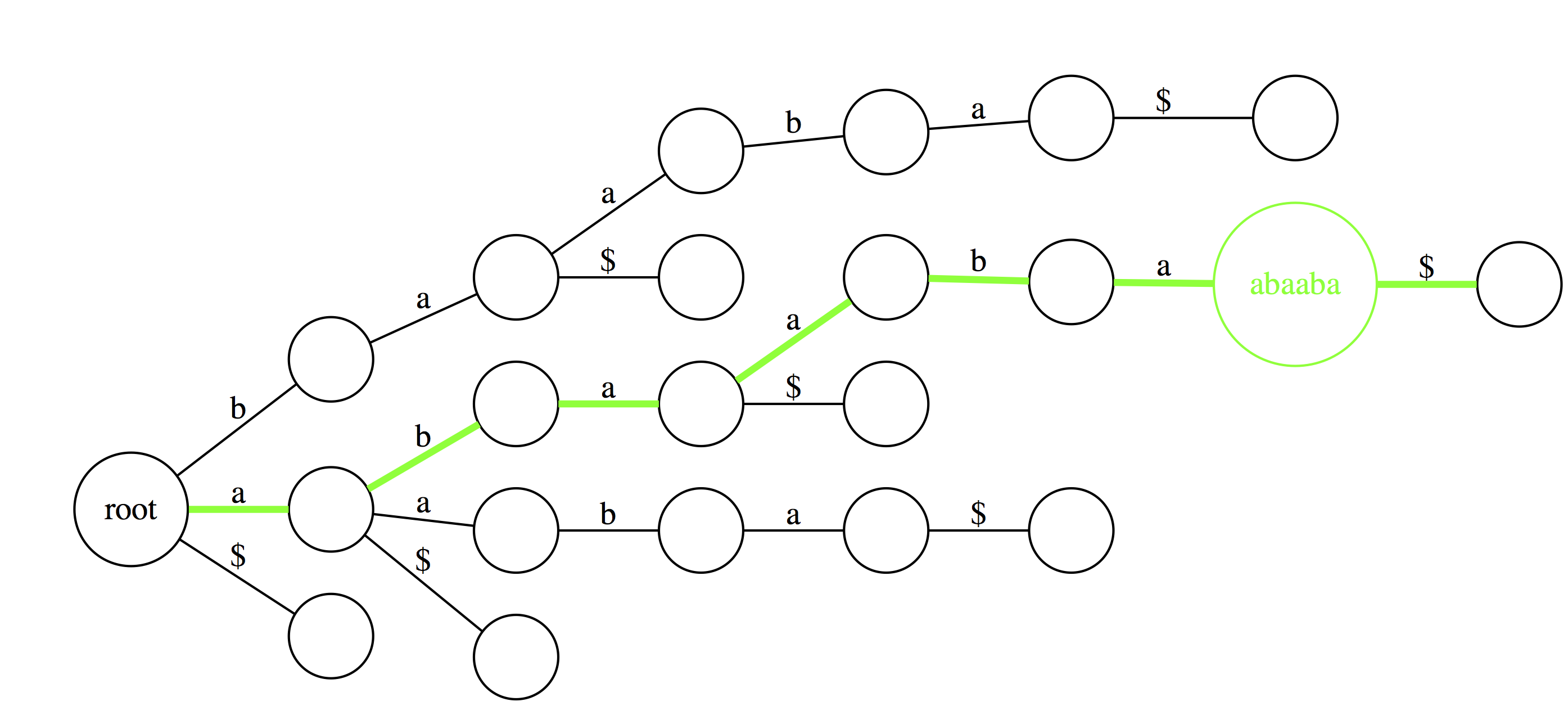Now let’s do the same for abaaba. Proceeding along the green path spells out all characters. Again, we conclude that abaaba is valid substring.
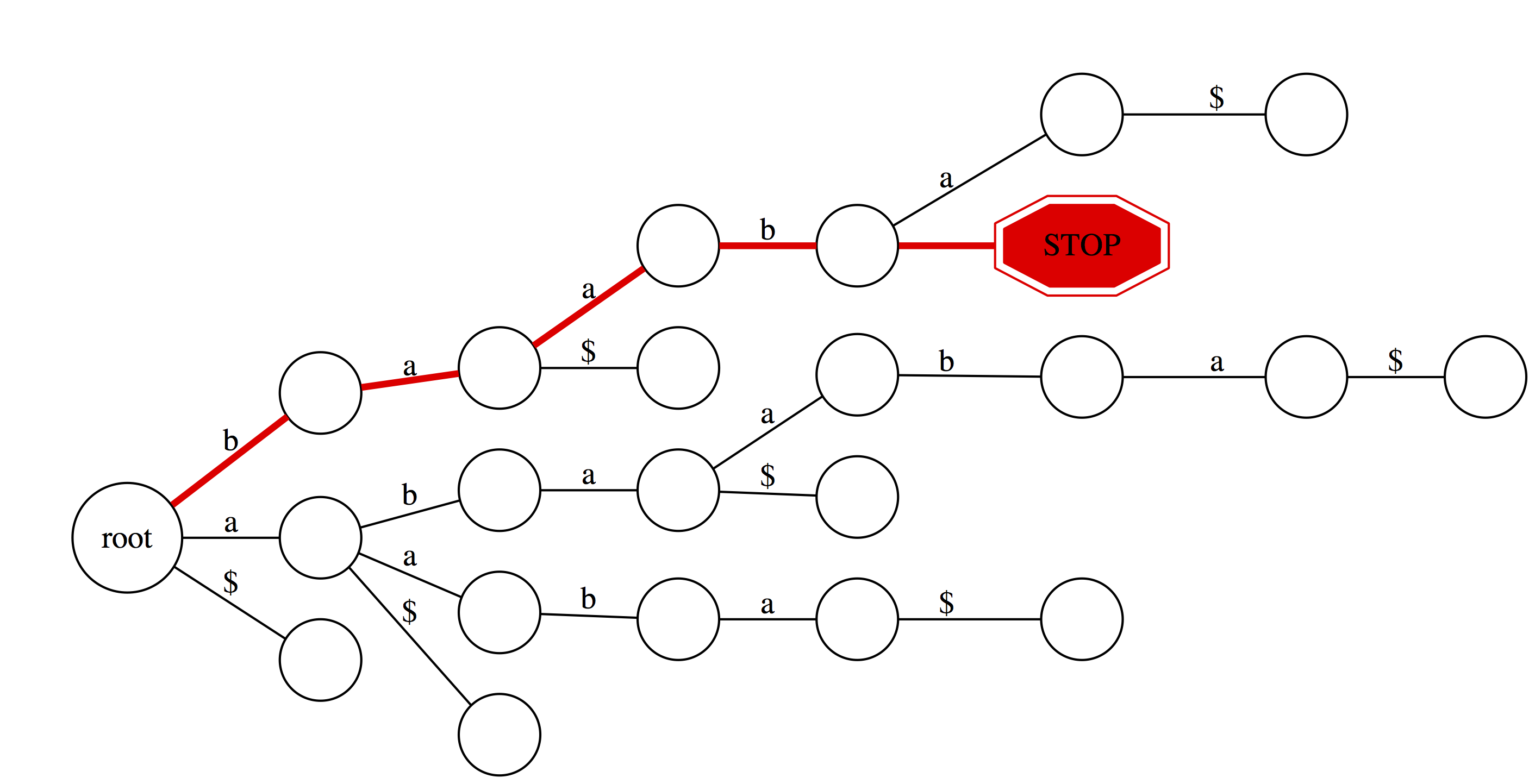But for baabb things look different. We proceed successfully (red path) through b, a, a, and b. However, there is no edge labeled b at baab node. Thus we fall off and conclude that baabb is not a substring of abaaba.
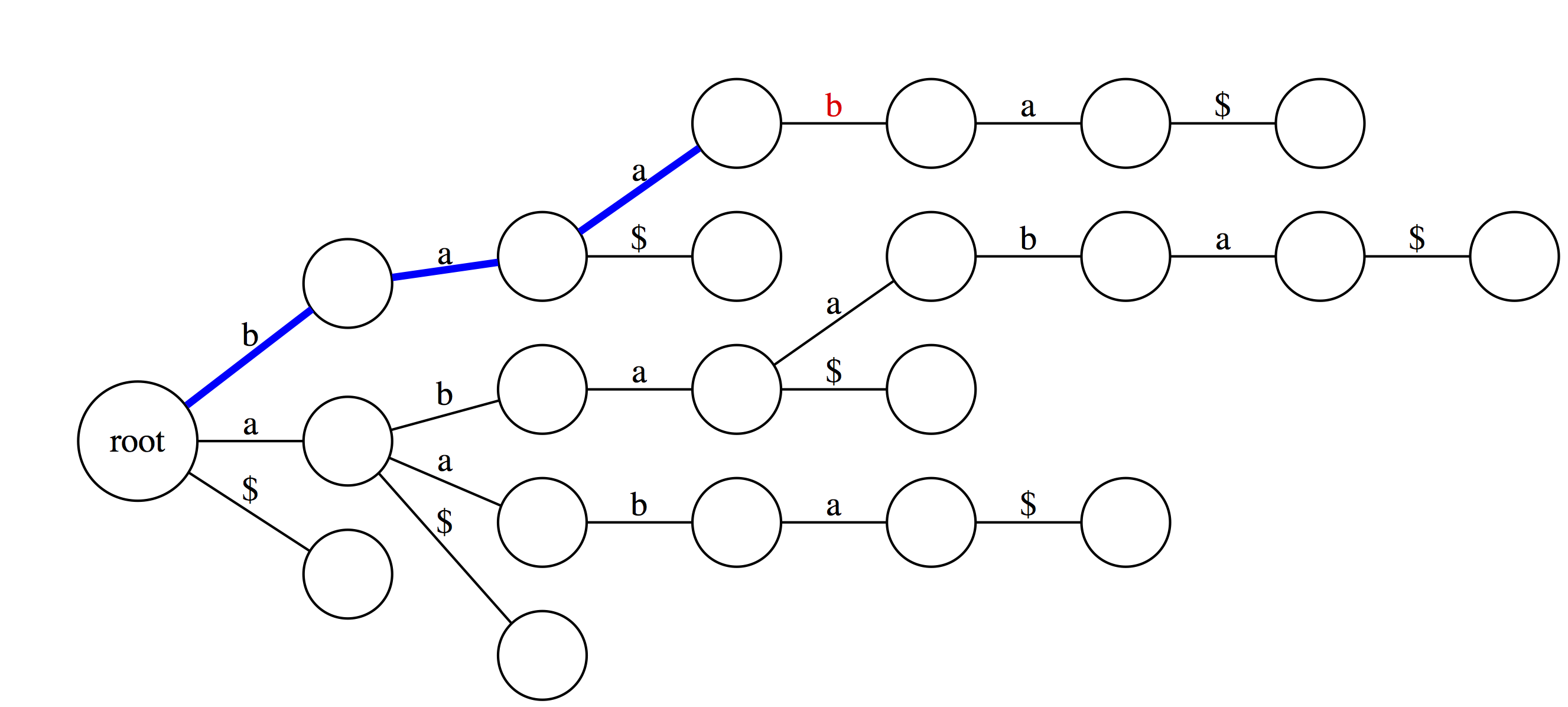We can also use suffix trie to check if a string is a suffix of a text. You can see that baa is not a suffix. This is because although it is valid substring, which traces a path through the trie, such path does not end with an outgoing edge labeled with $.
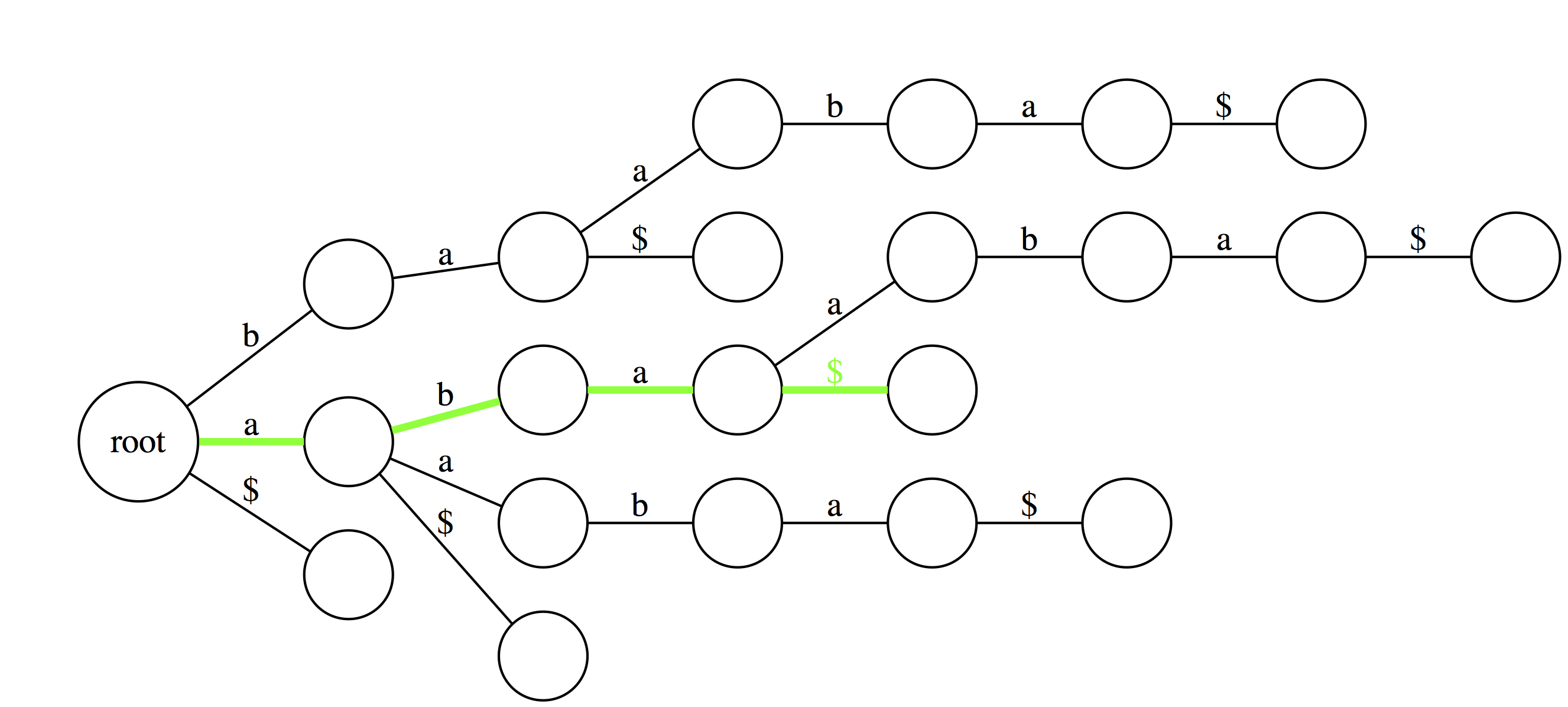Here aba is a suffix because one of the outgoing edges from the final node is labeled with $.
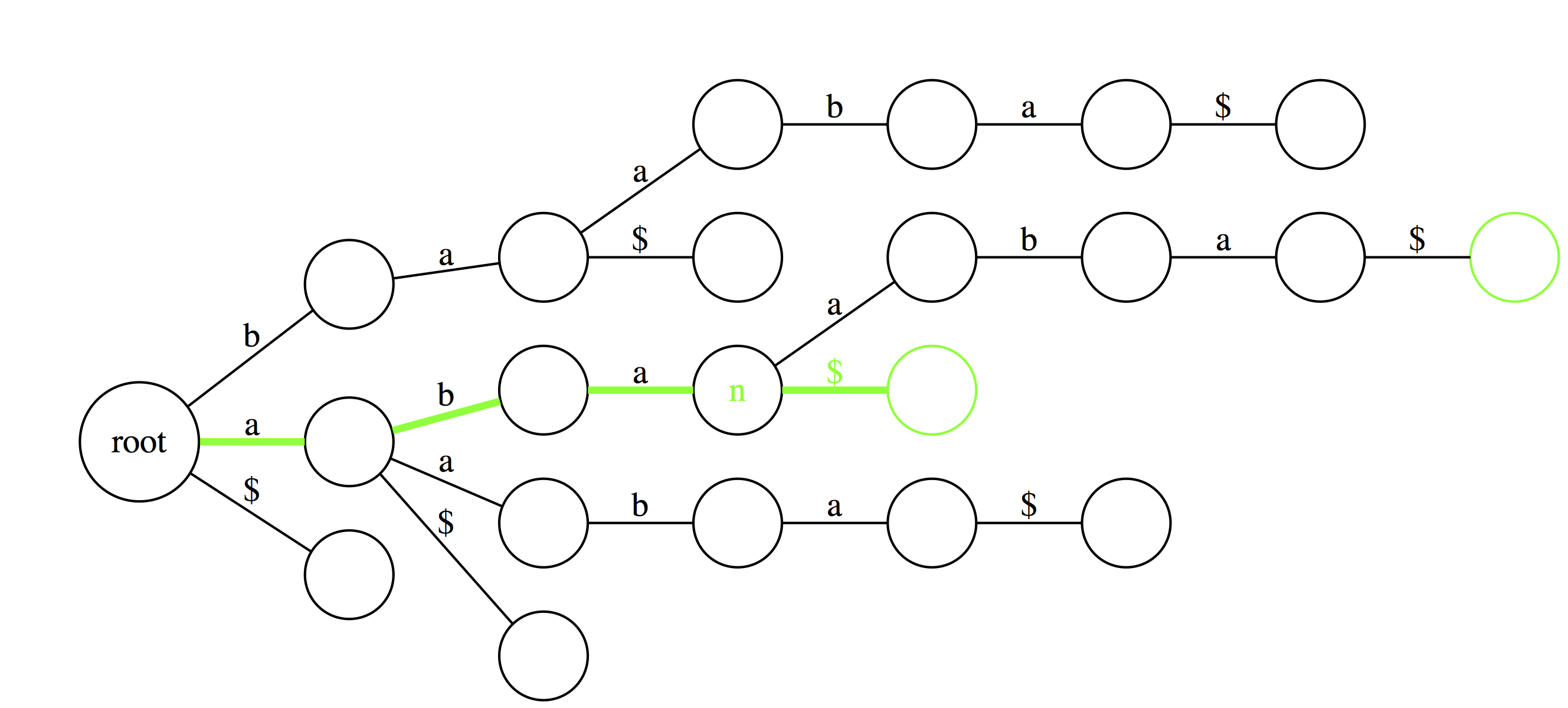Another useful feature of suffix trie is the ability to tell how many times a particular substring if found in a text. Here aba is found twice as the last edge of a path spelling aba leads to a node (n) with two outgoing edges.
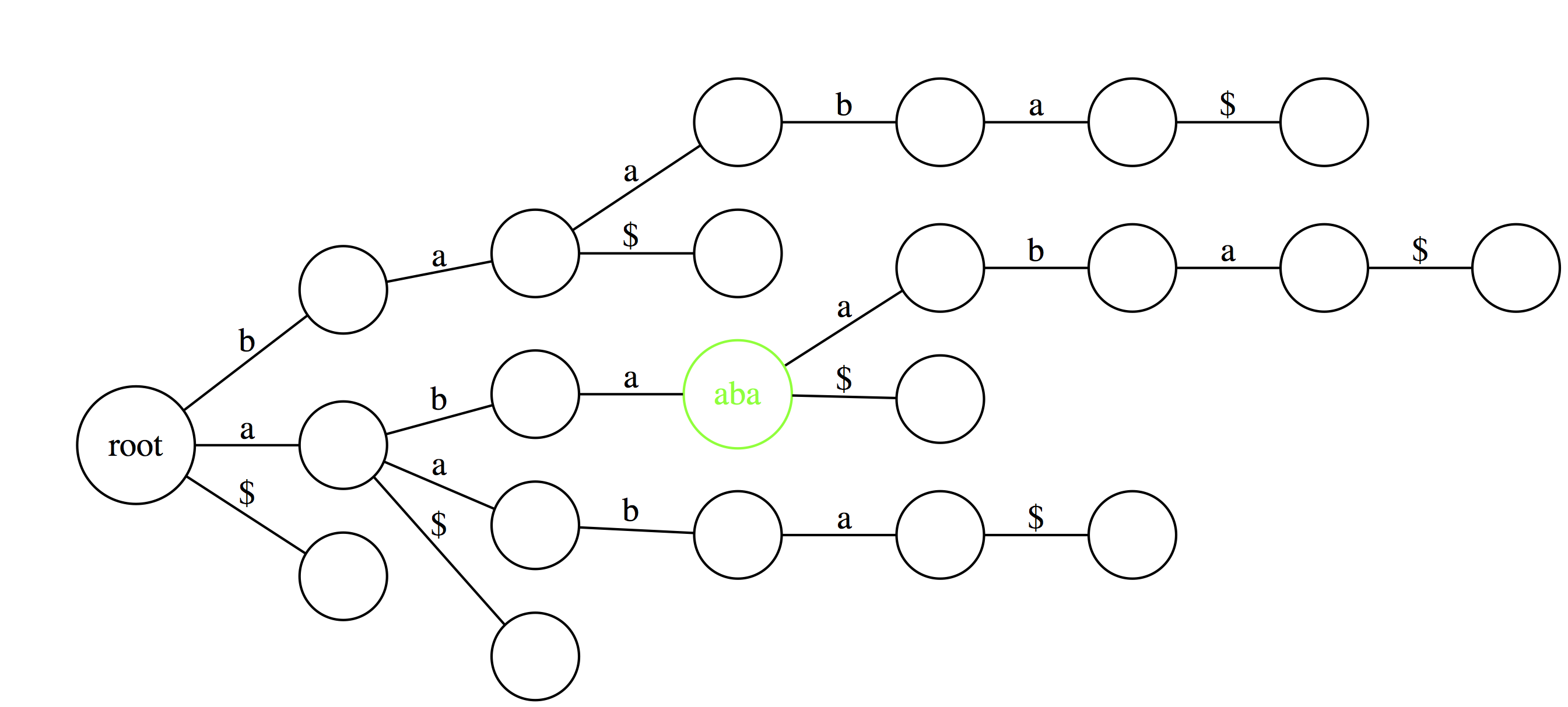Finally, similar logic allows to find the longest repeated substrings within a text. A deepest (furthest from the root) node with multiple outgoing edges wound point to a repetitive substring. Here aba is the longest repeated substring of abaaba.

Now that we explained how suffix tries can be used to find substrings in text, let’s reduce non-branching paths in tries and convert them to trees:

From a Trie to a Tree
If we collapse all non-branching paths and concatenate their labels we will get:
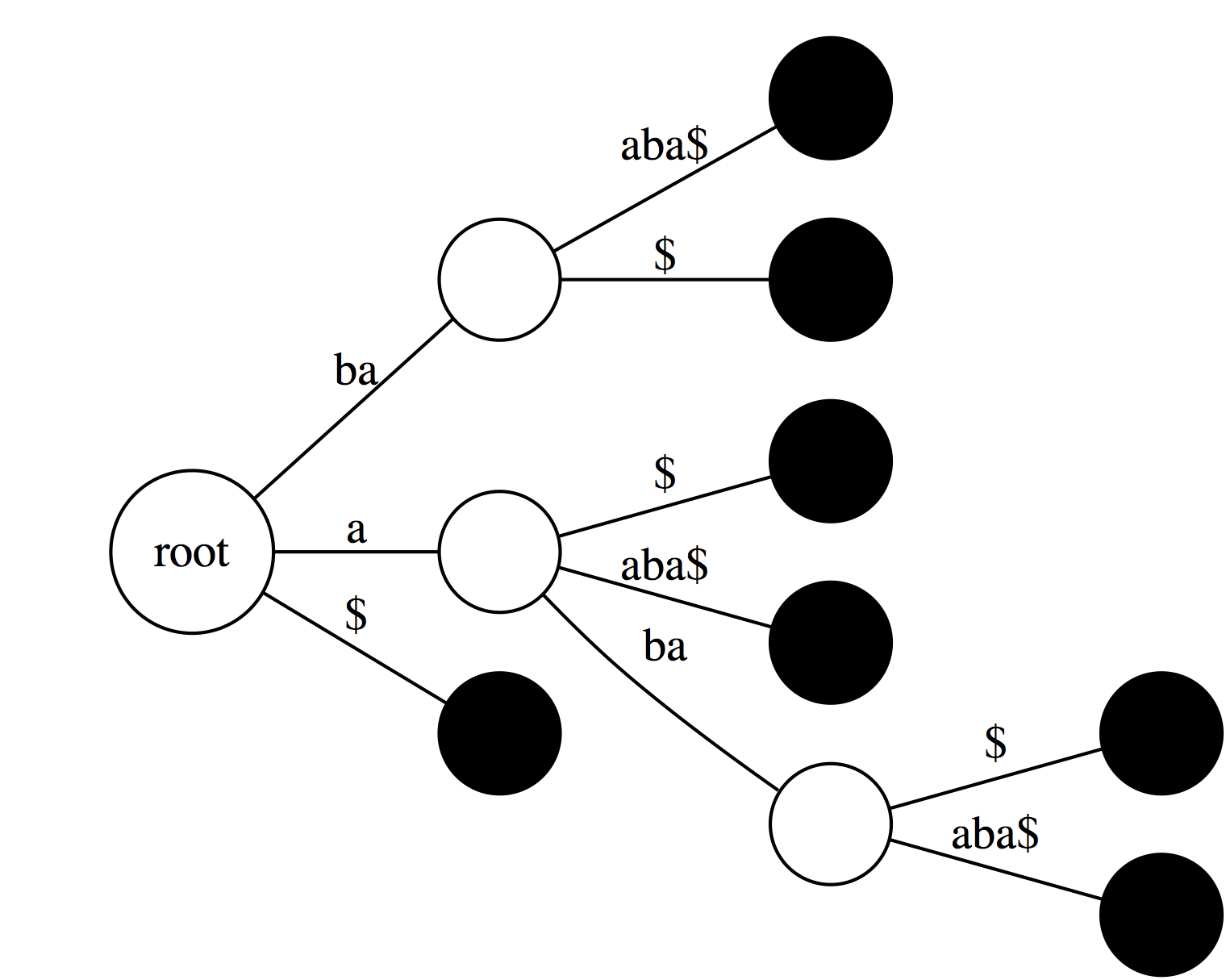Now, let’s label every leaf of the tree with offset (position in the text) of the corresponding suffix:
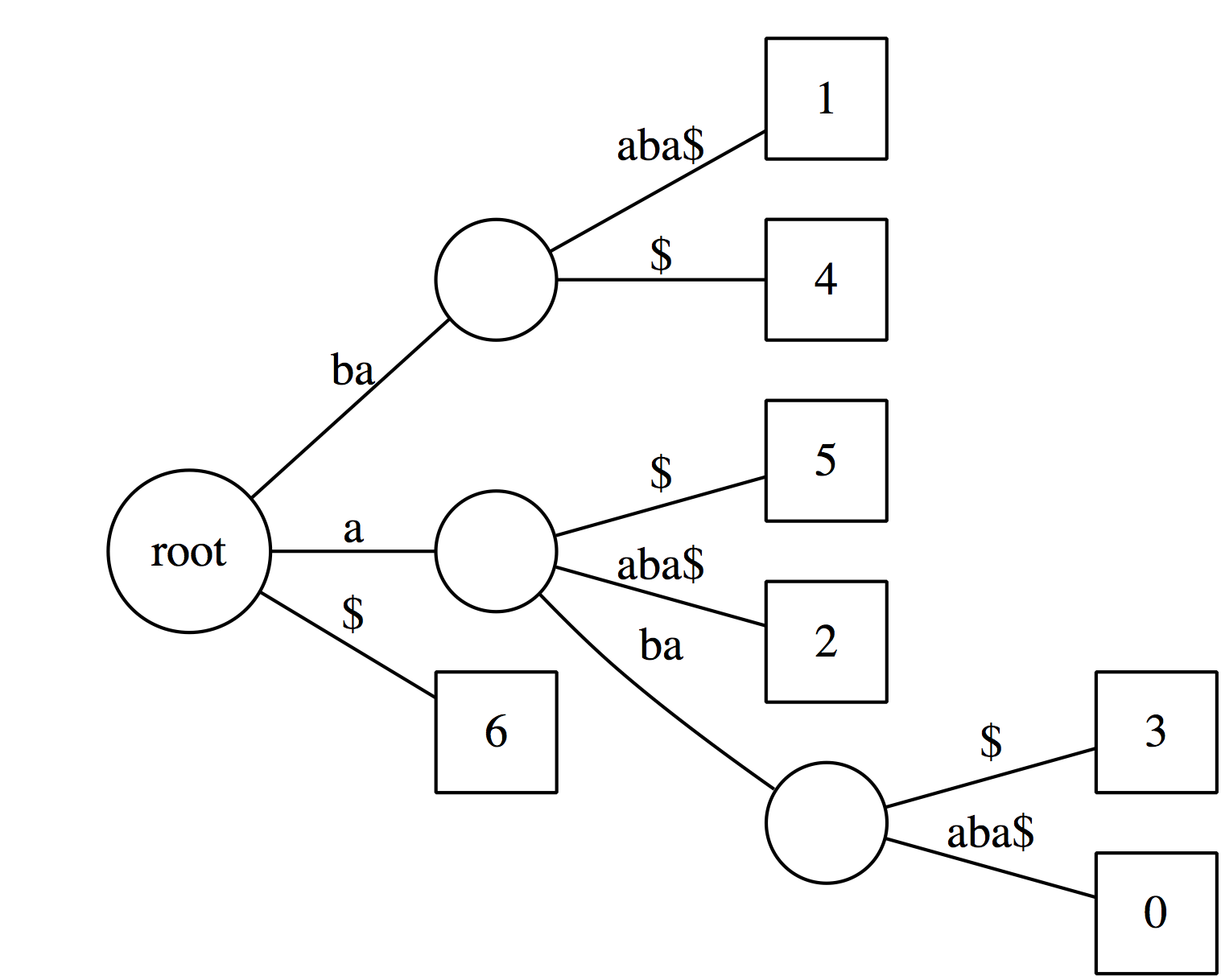Collapsing non-branching paths has given us a somewhat more compact data structure. Now see how we can use this data structure.

Looking for substrings in a Tree
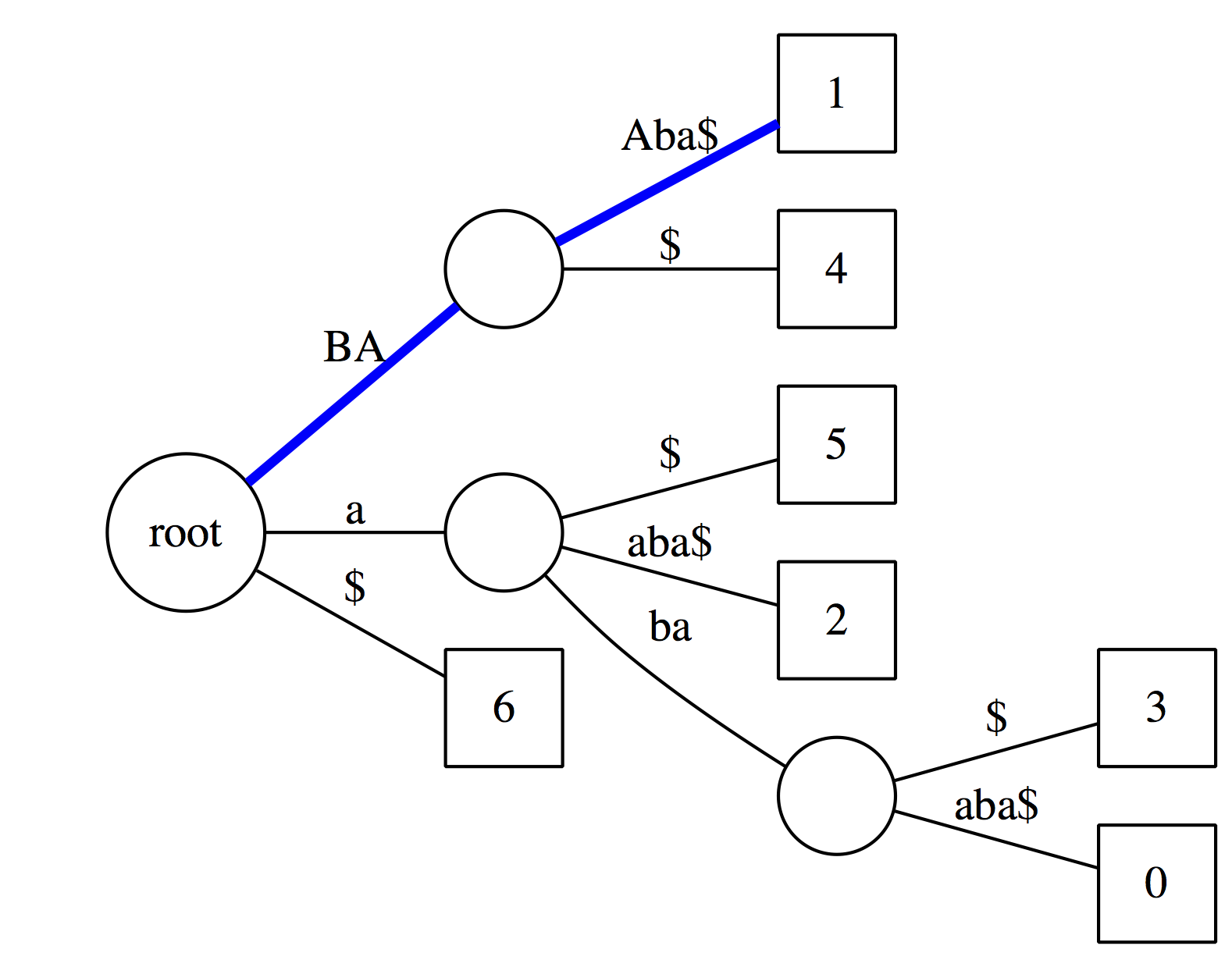Checking the above suffix tree to see if baa is a substring of the text. The logic is exactly the same as with suffix tries, except we now have to account for the fact that along some edges only a portion of the characters within a label will match. In this case matching characters are highlighted with uppercase: BA matches along the first edge along the blue path, and only A matches along the second edge. The conclusion is that baa is a substring of the text.
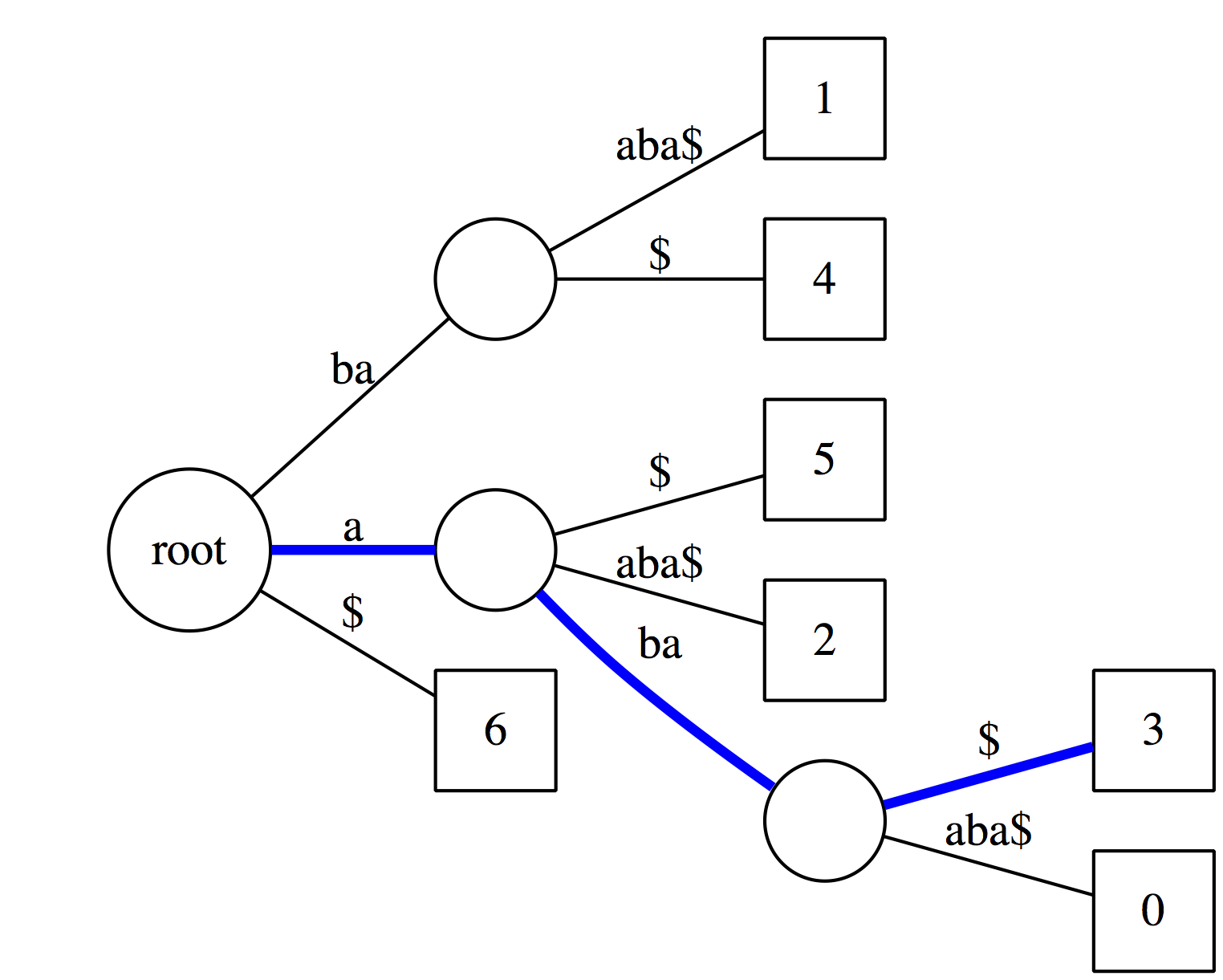Now let’s see if aba is a suffix of our text. It matches along the blue path and the last node along this path has an outgoing edge labeled with $. Thus it is a suffix.
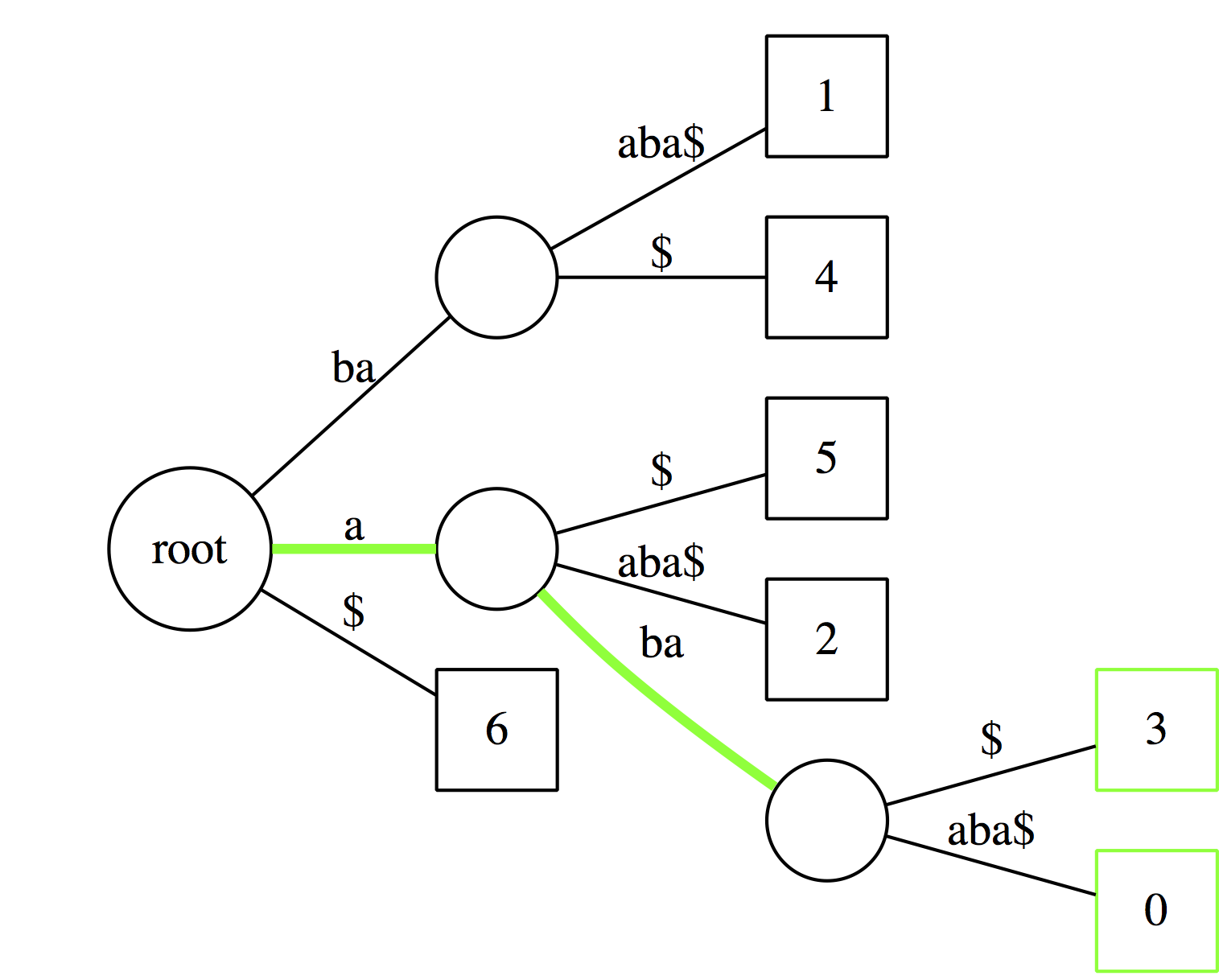And just like with suffix tries we can count occurrences of a substring by counting the number of outgoing edges from the last node.

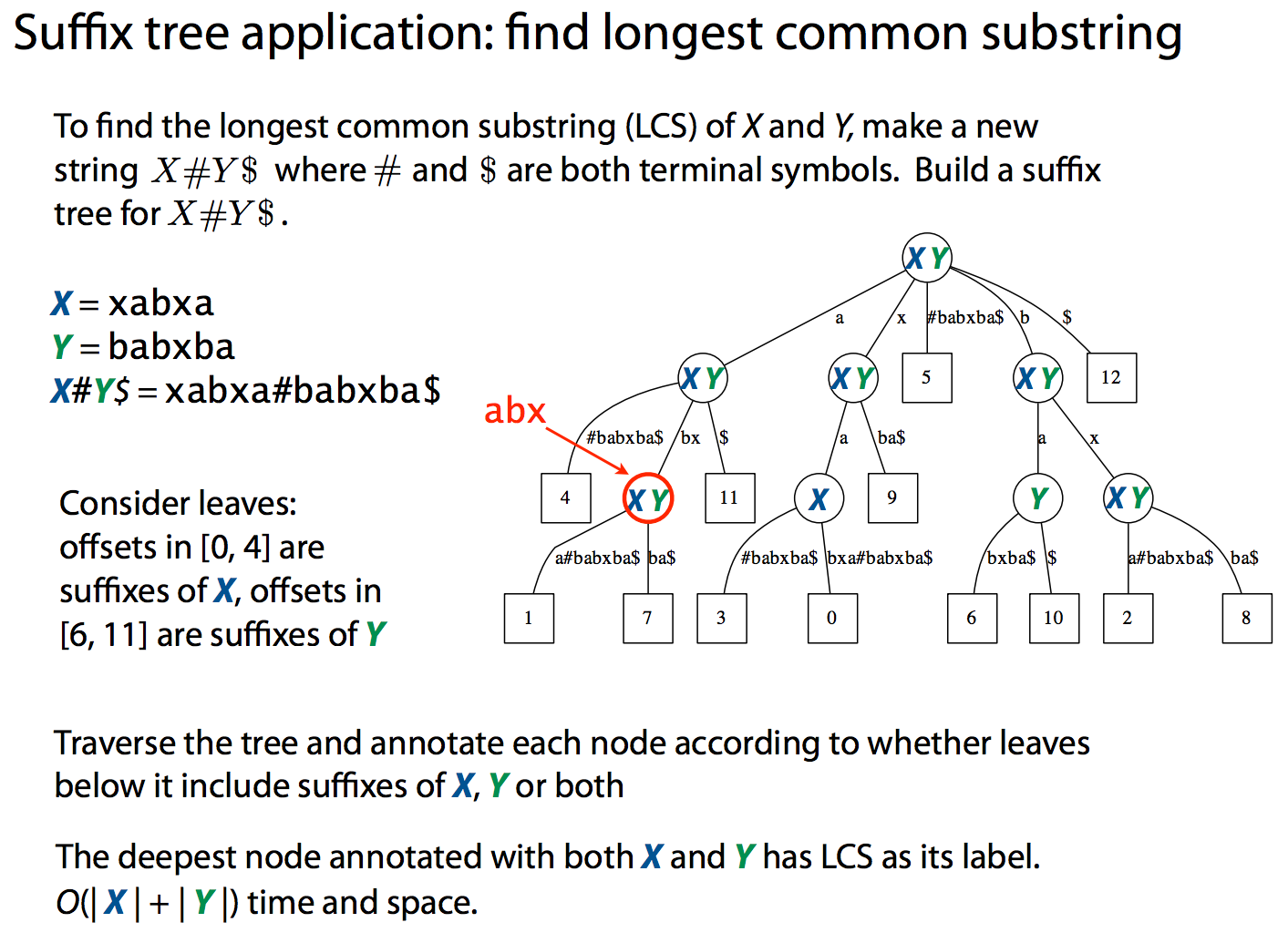
Application of suffix trees

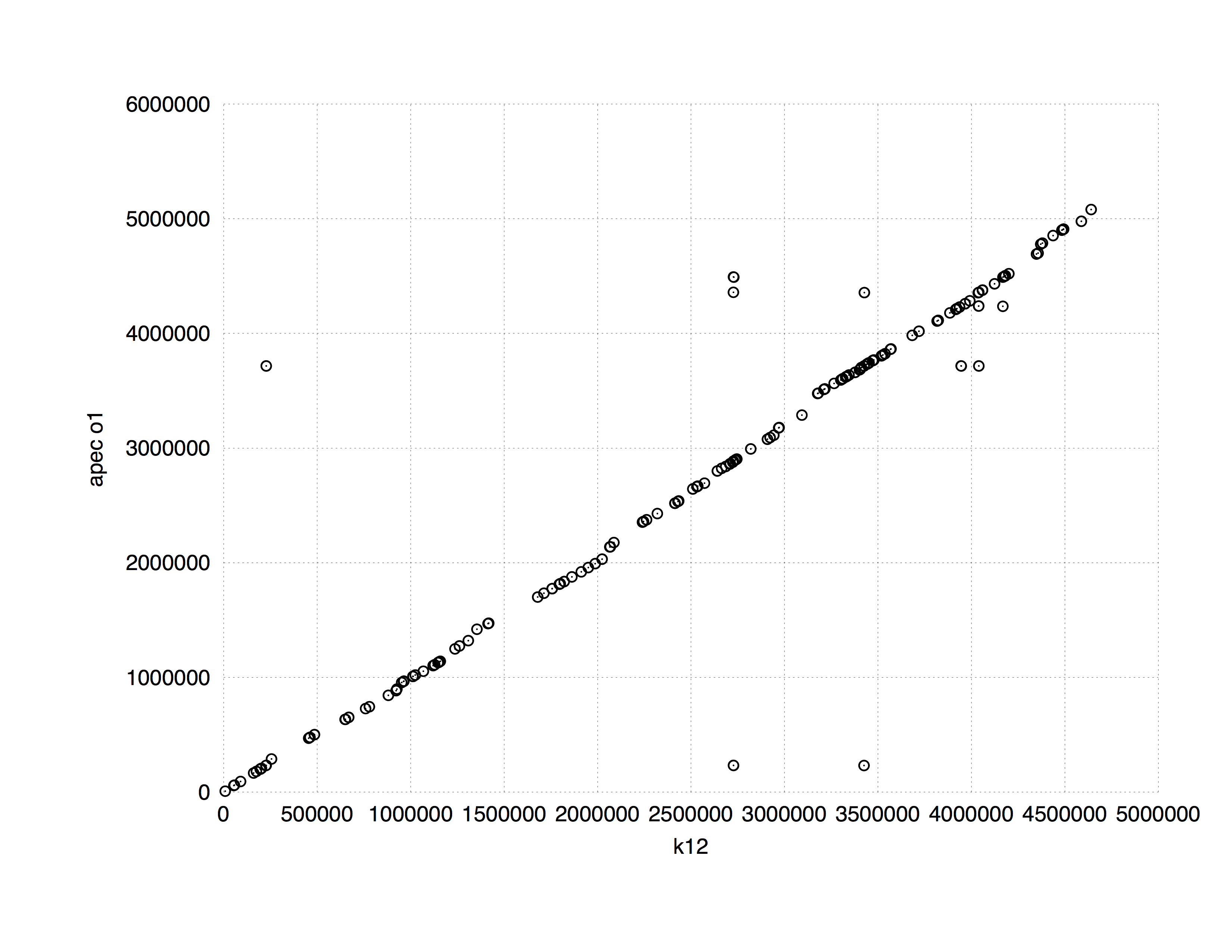
One of the common applications of suffix trees to the genome data analysis is finding (longest) common subsequences between two sequences. MUMMER implements this approach. The following plot shows a comparison between E. coli K12 and APEC O1 strains. It is computed in 8 seconds using approximately 10 Mb of RAM (K12 and APEC O1 genomes are 4.5 and 4.9. Mb, respectively).
To find longest common subsequences a suffix tree can be constructed from both sequences at once as shown in the following slide from Ben Langmead:
While suffix trees allow sequence comparisons to be performed in nearly linear time, they have large memory footprint. At some point this becomes a serious limitation making the use of suffix trees impractical. For example, indexing human genome will require ~47 Gb of memory.

Suffix arrays

Suffix array offers a more compact solution to representing text suffixes. It specified a lexicographic ordering of suffixes derived from text T$:
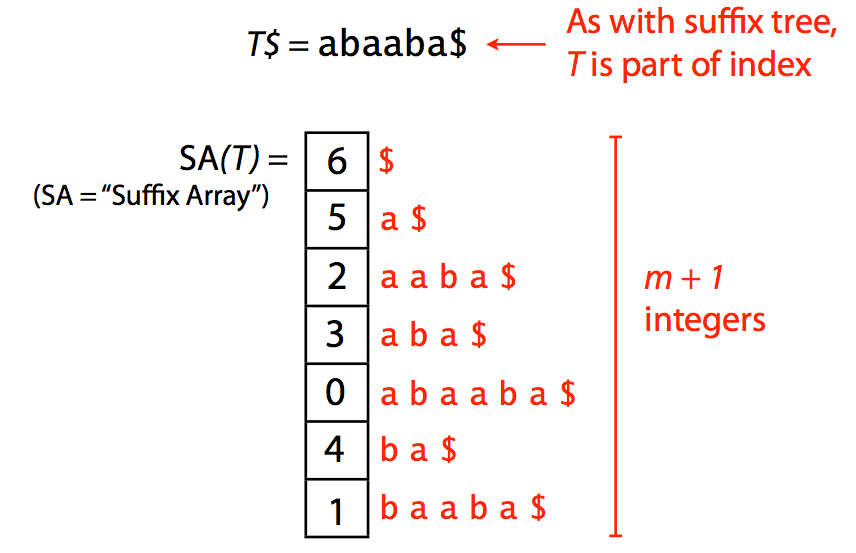A suffix array. Image by Ben Langmead

Because one does not need additional pointers required for tree representation, the suffix array (SA) has a significantly smaller memory footprint. For example, SA for human genome will occupy ~12Gb (down from 47Gb required for a suffix tree). Yet there is an even better idea.

Burrows-Wheeler Transform and FM index

Burrows-Wheeler (BW) transform is a reversible permutation of a string. For example, for a string:

abaaba$

create all rotations:

$abaaba
a$abaab
ba$abaa
aba$aba
aaba$ab
baaba$a
abaaba$

sort them lexicographically with $ as first character:

$abaaba
a$abaab
aaba$ab
aba$aba
abaaba$
ba$abaa
baaba$a

take the last column. It will be the BWT of the original string abaaba$:

abba$aa

Below is the entire procedure as one slide:
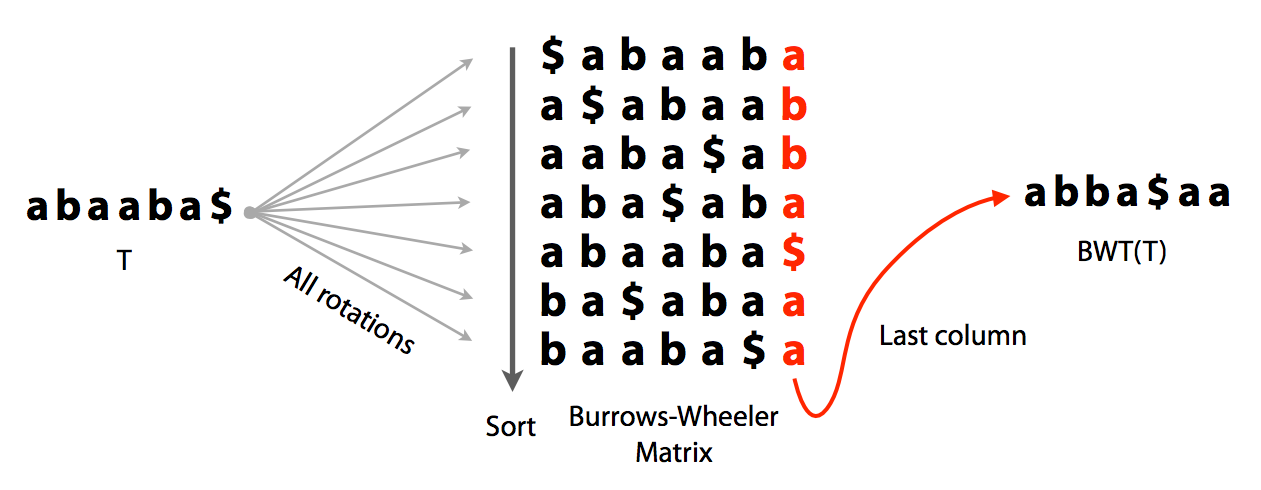Burrows-Wheeler transform. Image by Ben Langmead.

It has three important features that make it ideas for creating searchable compact representations of genomic data:

LF mapping of Burrows-Wheeler Matrix (BWM)

Let’s take the original string abaaba add $ and list charters ranks:

a0b0a1a2b1a3$

This ranking is done based on the order of the characters in the text (T-ranking). The order of ranked characters is preserved between the first column (F) and the last column (L):
LF mapping: as has the same order in F and L
LF mapping: bs has the same order in F and L. Image by Ben Langmead

Let’s now rank characters in order of their appearance in the sorted list of rotations (B-ranking):
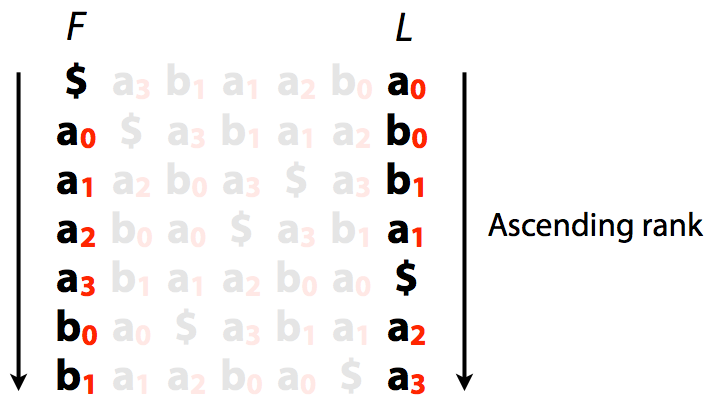Burrows-Wheeler transform with B-rankings. Image by Ben Langmead

A very important implication of this is that we can quickly jump from L to F:
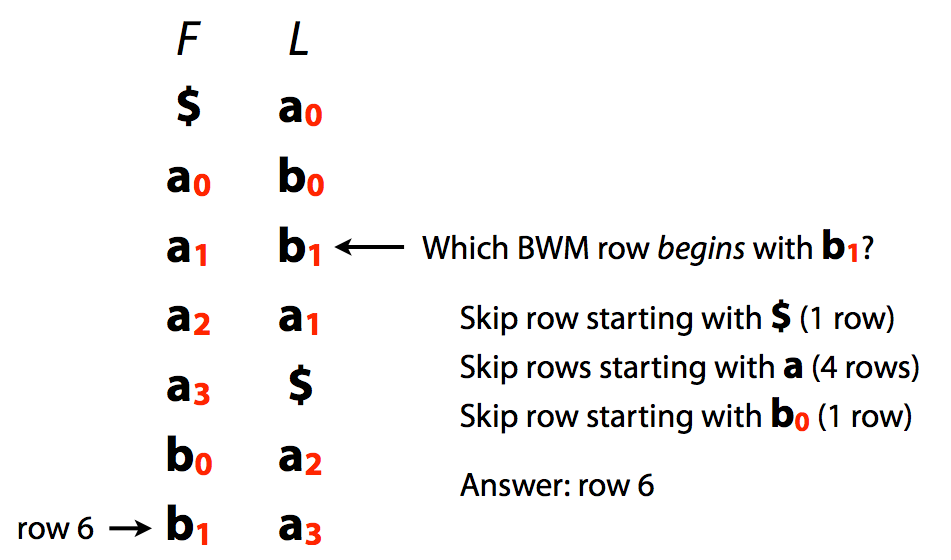L/F mapping. Image by Ben Langmead

Reversing BTW

Because of the LF mapping property was can also easily reconstruct original text from its BWT:
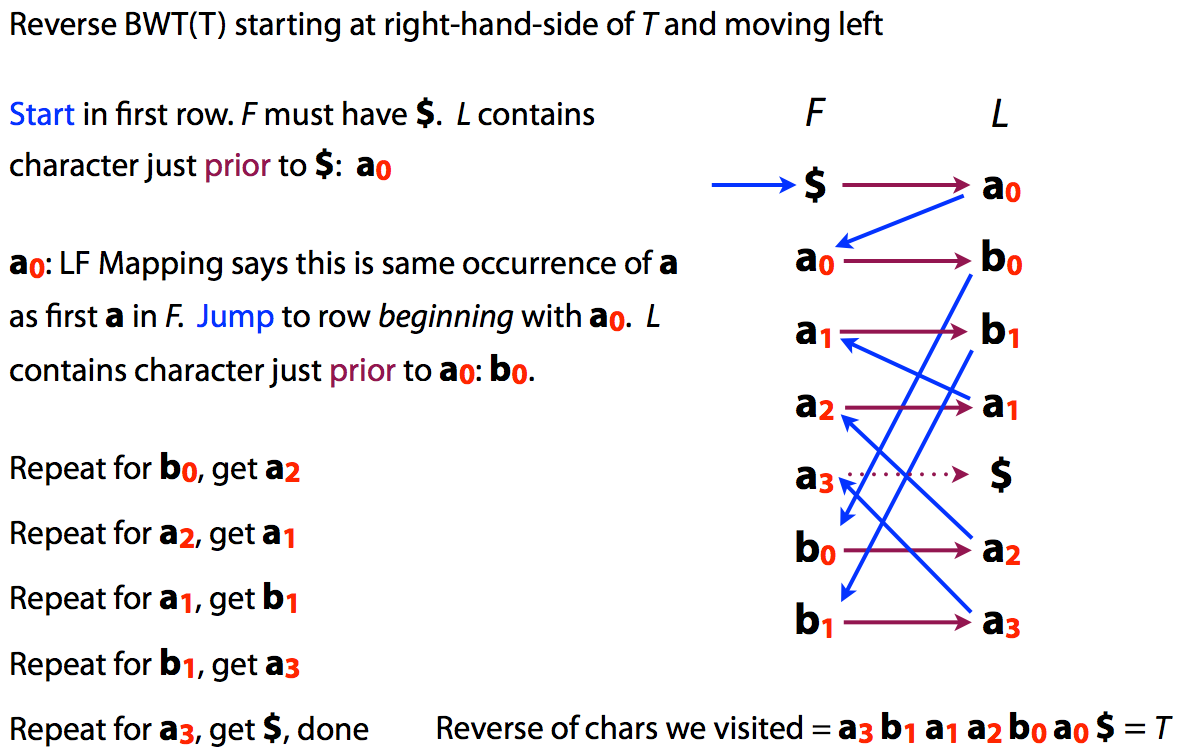or
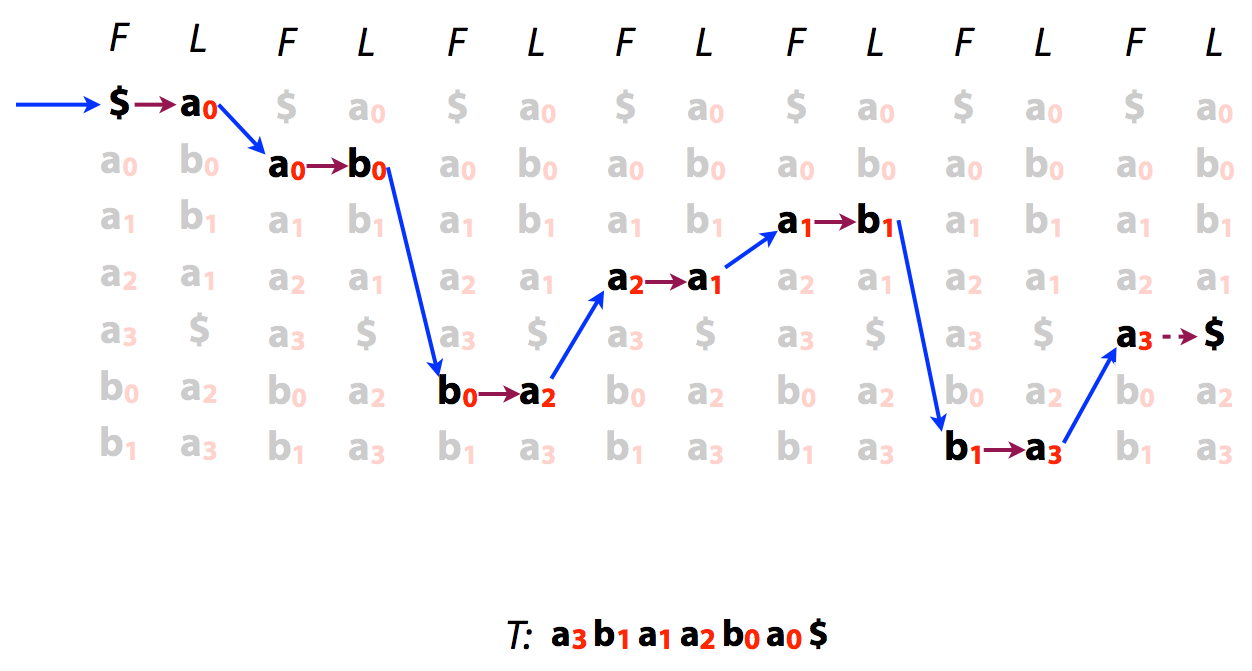Reversing BWT. Image by Ben Langmead

Searching BWT

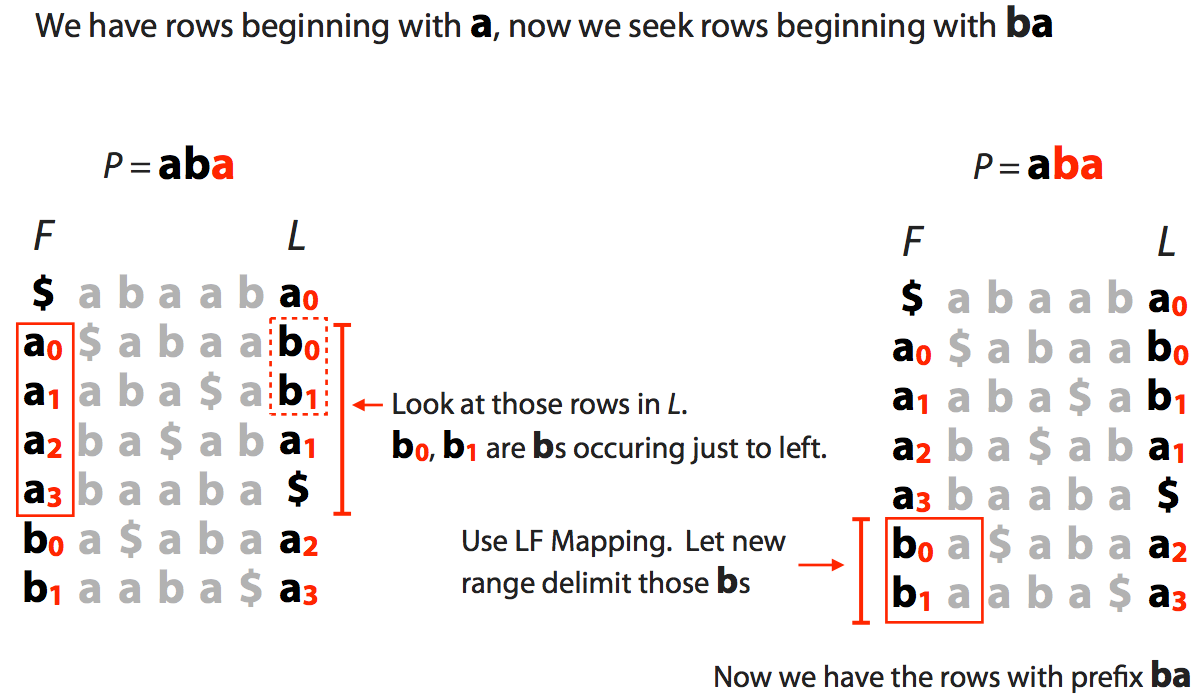
Let’s try to find is the string aba is present in a “genome” stored as a BWT.
We start with suffix of $ab\color{red}a$ shown in red. This gives us a range of characters in the F column (all as)
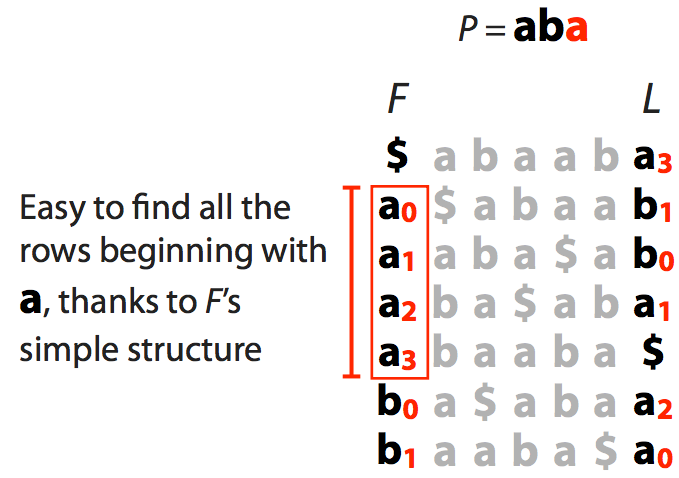We now extend to $a\color{red}{ba}$ and see how many of as have preceding bs:
Finally we extend to the entire string $\color{red}{aba}$:
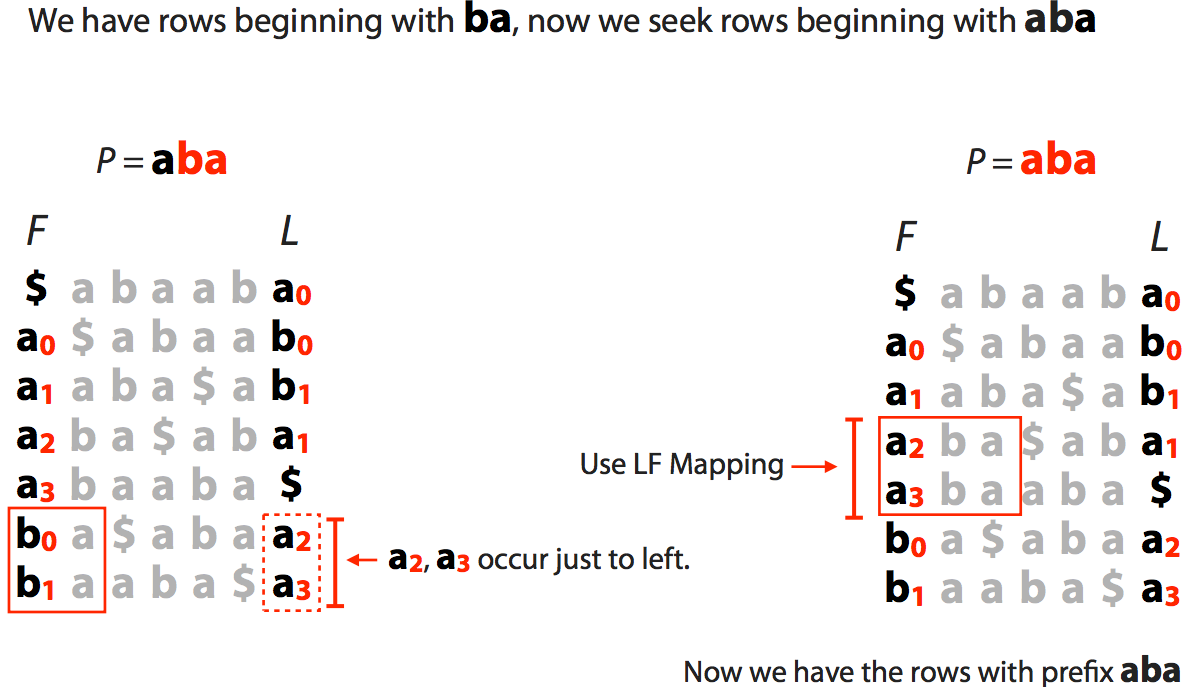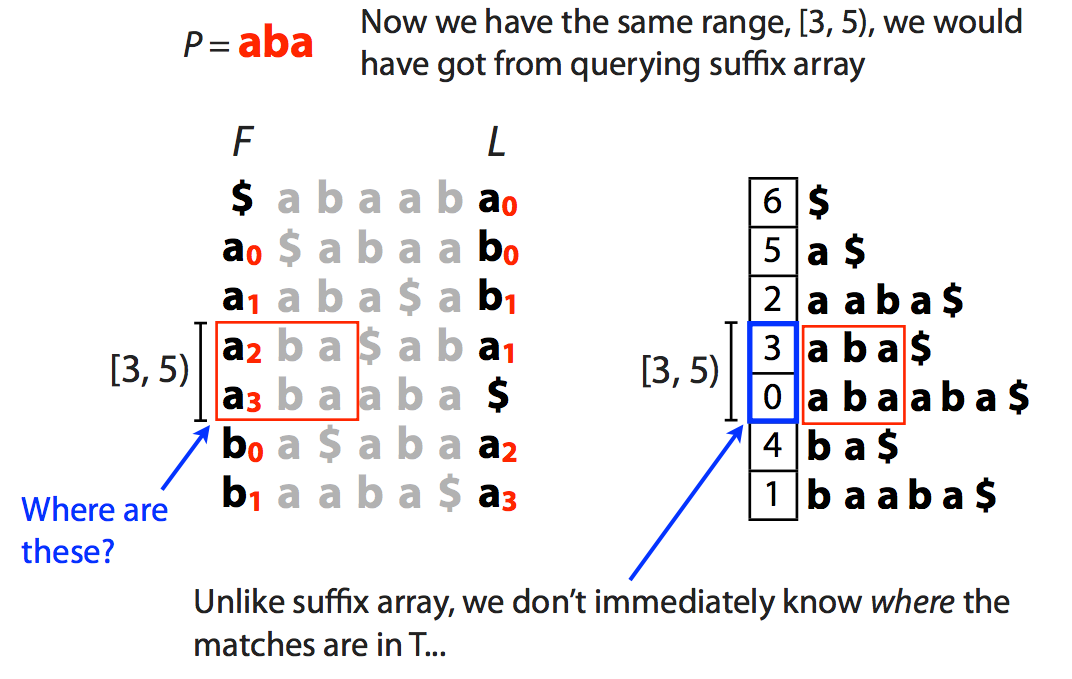
This tells us the range [3,5) but, as opposed to suffix array, this does not tell us where these matches occur in the actual sequence. We will come back to this problem shortly.
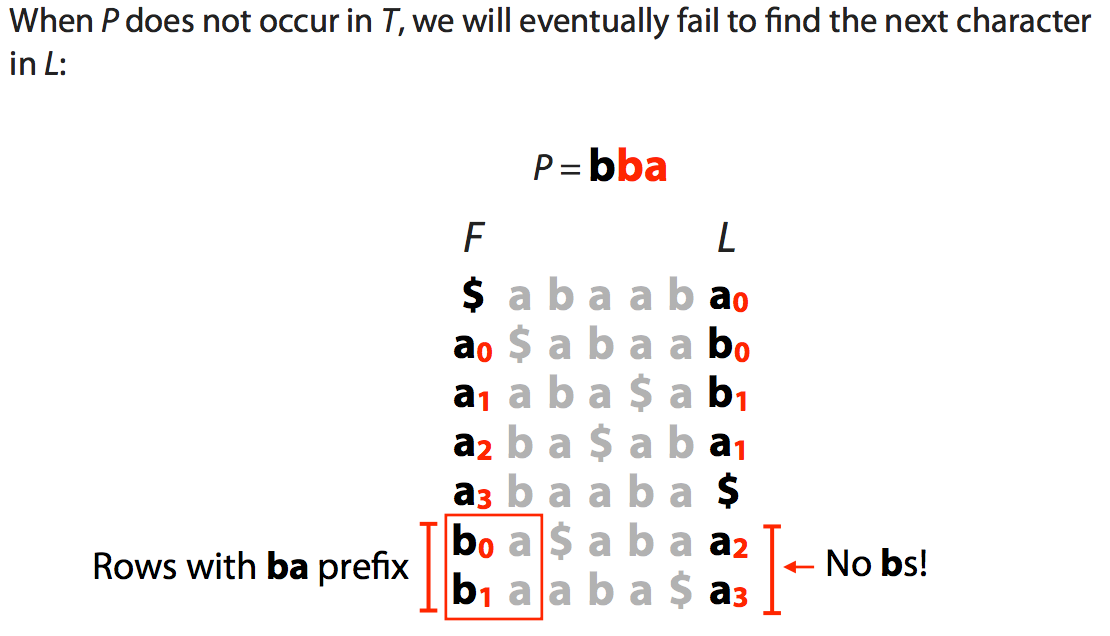
The slide below shows what happens when a match is not present in the “genome”:

Practicalities of using BWT

As we have seen BWT is very compact but has few shortcomings such as, for example, the difficulty is seeing where the matches are in the actual genome as well as some performance limitations. Combining BWT with auxiliary data structures creates FM-index (where FM stands for Full-text index in Minute space; curiously, the names of FM-index creators are Ferrigina and Manzini). The components of FM-index used for aligning reads to a genome are:

  BWT               Tally        Check    
                                 points 
                                                        SA
  F       L         a b          a b       SA           sample
  ---------        -----        -----     ----         --------
  $ abaab a         1 0          1 0       6 $          6
  a $abaa b         1 1                    5 a$         
  a aba$a b         1 2                    2 aaba$      2
  a ba$ab a         2 2          2 2       3 aba$       
  a baaba $         2 2                    0 abaaba$    0
> b a$aba a         3 2                    4 ba$        4
  b aaba$ a         4 2          4 2       1 baaba$

Where:

BWT

BWT - the BWT (L column from above) is stored and the first column (F) can be easily reconstructed as it is simply a list of all characters (4 in the case of DNA) and their counts.

Tally

Because we do not explicitly store ranks they can simply be obtained by counting occurrences of individual characters from the top of L column. Yet this is computationally expensive. Instead we store a tally table. At every row of the BWT matrix it shows how many times each character has been seen up to this point. For example at row marked with > there were 3 As and 2 Bs up to this point. In reality, to save space, only a subset of Tally entries is stored as Checkpoints recorded in regular intervals as shown above.

SA Sample

Finally, to find coordinates of matches in the genome offsets from an SA index are stored as SA sample (actual suffixes are not stored). This allows quickly finding location of a match within the genome by a direct look up. Similarly to Checkpoints only a fraction of these is stored to save space.

Thus the final list of components is:

For human genome with DNA alphabet of four nucleotides, saving checkpoint every 128th row, and saving SA offsets every 32nd row we will have: